第三回～調とは何か:スケールと調の関係を考える

制作に使える！コード理論:音楽理論の基礎を学ぼう

第1回第2回を通して音程とは何か、という話をしてきました。この概念はコード理論の扱う西洋音楽の全ての素となっていきます。

今回はその音程を規則的に並べることで生成される音階(Scale)そして、それから定められる調(Key)との関係を勉強していきましょう。

音階(Scale)とは何か

Scaleとは12音から任意の音を選び出し、並べた物と考えると分かりやすいかと思います
そもそもの定義はこれだけ…だから
12音全部！って欲張ってもスケールは成立します
クロマチックスケールって言いますね

で、もう少し音程という考え方に基づいて定義すると、ある法則で段階的に上行or下降する音の並び、とも言えます
音を選び出す、というよりも音と音の間隔に法則を付けて選び出します。

Major ScaleとMinor Scale

コード理論で扱う西洋音楽は数多のスケールの中でMajor ScaleとMinor Scaleを基礎的な音階と位置付けています。

そういう風になっているんです（強気）

五線譜に下から順番に音符を置くとメジャースケールになりますが、これはメジャースケールを頻繁に使うからこそ、記譜法がそのようになった、と言えるでしょう。

現時点では調とは、あるメジャー、マイナースケールが支配的な曲(もしくは曲の一部分)としておきましょう。

Major Scaleの例

まず簡単なCmajorスケールを見てみましょう

さてこのCMajorScaleですが、スケールの最初の音、基準となる音、主音（Tonic）と言いますが、ここから各音同士の距離を見て行きましょう。

ド→レ　全音
レ→ミ　全音
ミ→ファ半音
ファ→ソ全音
ソ→ラ　全音
ラ→シ　全音
シ→ド　半音

並べると全全半全全全半となっています。
この法則の積み重ねで出来ている音階の事をメジャースケールと言います。

Tonicの音＋スケール名で、今回の場合はCメジャースケールと言います。

コード理論で扱う西洋音楽は、調性音楽と呼ばれ（重要なので何回も言う）、このメジャースケールとマイナースケールを基本にして成り立っています。

ですので、主に使われているスケールがCメジャースケールである時、KeyCと書き
Cメジャーキー（ハ長調）である、と言えるわけです。

＊調とは何か、にはやや定義の揺れがありました。後日しっかり解説しますが常用においてはこの解釈で問題無いと思います＊

Minor Scaleの例

今回も簡単のためにAminorスケールを採用します。（臨時記号使わないので）

さてAマイナースケールを見て行きましょう

ラ→シ　全音

シ→ド　半音

ド→レ　全音

レ→ミ　全音

ミ→ファ半音

ファ→ソ全音

ソ→ラ　全音

並べると

全半全全半全全となります。

この法則の積み重ねで出来ている音階の事をマイナースケールと言います。

Tonicの音＋スケール名で、今回はAマイナースケールと言います。

マイナースケールの特徴としては、あるメジャースケールの第六音からの順番と同一である事が特徴です。

実際にCメジャースケールとAマイナースケールはそのような関係になっています。

この二つの音階の関係の事をRelative Scaleと呼びます。ただし日本語的には平行調という呼称が用いられる事もあるので注意が必要です。

この様に全音二つ半音全音三つ半音という間隔で構成される音階をダイアトニックスケールと呼びます。

全てはメジャースケールと、マイナースケールを中心に話は動くんだという風に認識して貰えれば大丈夫です。（これはコードの話に入っても続けて持っていて欲しい話です）

また一部の理論の流派ではマイナーKey表記は用いない（構成音的にはメジャーと同一なので）のもありますが、ここでは使って行きたいと思います。

メジャースケールの生成と調号の関係

さて譜面上で一番簡単に表す事が出来るCメジャースケールと、Aマイナースケールについて解説しました。メジャースケールの特性から、12音の上に違ったメジャースケールが生成可能である事が分かるかと思います。

もちろん闇雲にTonicを選んでスケールを生成しても良いのですが、折角なのでCメジャースケールを簡単に”修正”する形で残りのスケールを紐解いて行きたいと思います。

改めてメジャースケールの各音毎の音程を確認すると

全全半全全全半

という並びになっています。さてどこから始めるのが一番修正が少なく済むでしょうか。

正解は二つ

第四音から初めて第七音を半音下げる、こうすると

全全半全（元々半音間隔だった物が下に一個ずれたので全音に広がる）

そして全全半となります。

こうする事でCメジャースケールの第七音であったB音に♭を付ける事でFメジャースケールが完成します。

ここで調号の話が登場します。例えば今目の前の曲がFメジャースケールを基調とするKey Fであった場合、今の場合いちいちB音に♭をつけないといけない。

これ非常に面倒ですよね。なので楽譜の最初に♭を付けてしまおうというのが調に合わせた調号です。

同じ操作を同様に繰り返すとFメジャースケールの第4音B♭から始まり、Fメジャースケールの第七音に♭、つまりEに♭が付きますね。こうしてB♭メジャースケールが出来ると。

この様にTonicをCメジャーから4度動かす（5度下降させる）事によって一つずつ調号が増えて行きます。当然毎回同じ度数の音に♭が付いていく訳なので、調号が付く場所も五度ずつの間隔になっているはず…

B♭→E♭→A♭→D♭…

この事から調号からその楽曲の基本的なキーが判明し、また主に使われる音階が分かります。（後々触れますが転調した、と作曲者が判断した場合は調号を変更しています。）

同様にCメジャースケールを完全五度上、Gから並び替えてメジャースケールを作って行きましょう。こうするとCメジャースケールの第四音Fに♯が付く事が分かるかと思います。（実際に手を動かして確認する事をおすすめします）

シャープが増えて行く方向にも次々にメジャースケールが生成する事が可能です。

本来、♭系と♯系で12個ずつのメジャースケールが生成されますが、途中で同じもの（被り）が生まれてきます。

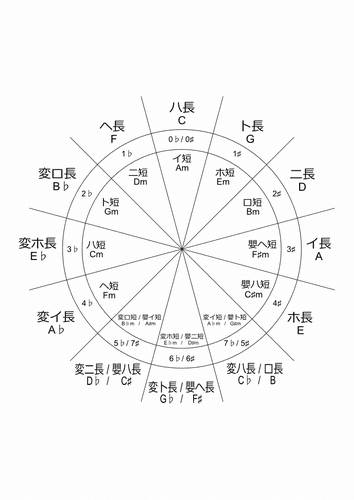
Cirle of Fifth（五度圏）

という事で♭系と♯系の調の関係をまとめた物が良く言われるCircle of Fifth（五度圏）と言われる物です。

この様に西洋音楽においてはC～Bまでの全12音を元とした、長音階、短音階が全24個存在し、それぞれの音階を基にした調が24調存在します。

この五度圏の表は、12調でのスケール練習などで絶大な効力を発揮するのでネットに沢山落ちてる五度圏表でも良いし、自分でも作っても良いので気に入った物を1つ持っておくと良いでしょう。

まとめ

調性音楽という物の中心にメジャースケールとマイナースケールが置かれているという事が身に染みれば今回の記事は概ね理解出来たと言えるのではないでしょうか。

この中心におかれているメジャースケールと、マイナースケールに含まれている音を使ってコードを作ったりメロディーを作ったり…という話がこの先割と続きます。

分からなくなったらこの記事に、この記事が分からなくなったら音程の記事に戻って貰えたら理解しやすいかと思います。
制作に使える！コード理論:音楽理論の基礎を学ぼう